Dream & Passion: [Basic] Whitening

whiten.pdf (37 KB)

From: http://cis.legacy.ics.tkk.fi/aapo/papers/IJCNN99_tutorialweb/node26.html

Another useful preprocessing strategy in ICA is to first whiten the observed variables. This means that before the application of the ICA algorithm (and after centering), we transform the observed vector ${\bf x}$ linearly so that we obtain a new vector $\tilde{{\bf x}}$ which is white, i.e. its components are uncorrelated and their variances equal unity. In other words, the covariance matrix of $\tilde{{\bf x}}$ equals the identity matrix:

$\begin{displaymath}E\{\tilde{{\bf x}}\tilde{{\bf x}}^T\}={\bf I}. \end{displaymath}$

(30)

The whitening transformation is always possible. One popular method for whitening is to use the eigen-value decomposition (EVD) of the covariance matrix $E\{{\bf x}{\bf x}^T\}={\bf E}{\bf D}{\bf E}^T$ , where ${\bf E}$ is the orthogonal matrix of eigenvectors of $E\{{\bf x}{\bf x}^T\}$ and ${\bf D}$ is the diagonal matrix of its eigenvalues, ${\bf D}= \mbox{diag}(d_1,...,d_n)$ . Note that $E\{{\bf x}{\bf x}^T\}$ can be estimated in a standard way from the available sample ${\bf x}(1), ... , {\bf x}(T)$ . Whitening can now be done by

$\begin{displaymath} \tilde{{\bf x}}={\bf E}{\bf D}^{-1/2}{\bf E}^T {\bf x} \end{displaymath}$

(31)

where the matrix ${\bf D}^{-1/2}$ is computed by a simple component-wise operation as ${\bf D}^{-1/2}=\mbox{diag}(d_1^{-1/2},...,d_n^{-1/2})$ . It is easy to check that now $E\{\tilde{{\bf x}}\tilde{{\bf x}}^T\}={\bf I}$ .

Whitening transforms the mixing matrix into a new one, $\tilde{{\bf A}}$ . We have from (4) and (34):

$\begin{displaymath}\tilde{{\bf x}}= {\bf E}{\bf D}^{-1/2}{\bf E}^T {\bf A}{\bf s}=\tilde{{\bf A}}{\bf s} \end{displaymath}$

(32)

The utility of whitening resides in the fact that the new mixing matrix $\tilde{{\bf A}}$ is orthogonal. This can be seen from

$\begin{displaymath}E\{\tilde{{\bf x}}\tilde{{\bf x}}^T\}=\tilde{{\bf A}} E\{{\bf... ...\}\tilde{{\bf A}}^T =\tilde{{\bf A}}\tilde{{\bf A}}^T={\bf I}. \end{displaymath}$

(33)

Here we see that whitening reduces the number of parameters to be estimated. Instead of having to estimate the n² parameters that are the elements of the original matrix ${\bf A}$ , we only need to estimate the new, orthogonal mixing matrix $\tilde{{\bf A}}$ . An orthogonal matrix contains n(n-1)/2degrees of freedom. For example, in two dimensions, an orthogonal transformation is determined by a single angle parameter. In larger dimensions, an orthogonal matrix contains only about half of the number of parameters of an arbitrary matrix. Thus one can say that whitening solves half of the problem of ICA. Because whitening is a very simple and standard procedure, much simpler than any ICA algorithms, it is a good idea to reduce the complexity of the problem this way.

It may also be quite useful to reduce the dimension of the data at the same time as we do the whitening. Then we look at the eigenvalues d_j of $E\{{\bf x}{\bf x}^T\}$ and discard those that are too small, as is often done in the statistical technique of principal component analysis. This has often the effect of reducing noise. Moreover, dimension reduction prevents overlearning, which can sometimes be observed in ICA [26].

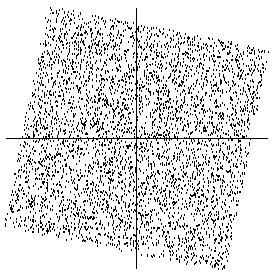
A graphical illustration of the effect of whitening can be seen in Figure 10, in which the data in Figure 6 has been whitened. The square defining the distribution is now clearly a rotated version of the original square in Figure 5. All that is left is the estimation of a single angle that gives the rotation.

Figure 10: The joint distribution of the whitened mixtures.

$\resizebox{.50\textwidth}{!}{ \includegraphics{Vuni}}$

In the rest of this tutorial, we assume that the data has been preprocessed by centering and whitening. For simplicity of notation, we denote the preprocessed data just by ${\bf x}$ , and the transformed mixing matrix by ${\bf A}$ , omitting the tildes.

Posted via email from Troy's posterous

Thursday, December 16, 2010

[Basic] Whitening

No comments:

Post a Comment