Super Crazy Guitar Maniac DLX3

Guitar playing game.

Line Rider

A small flash game.

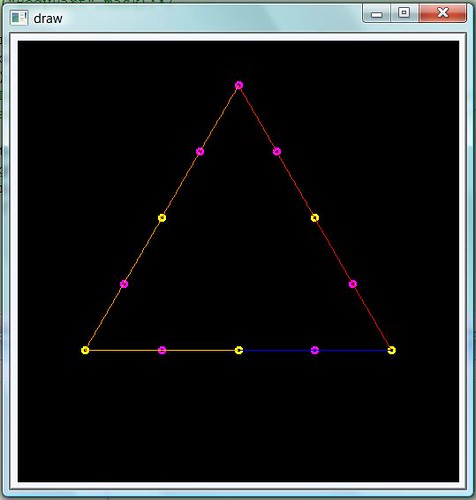
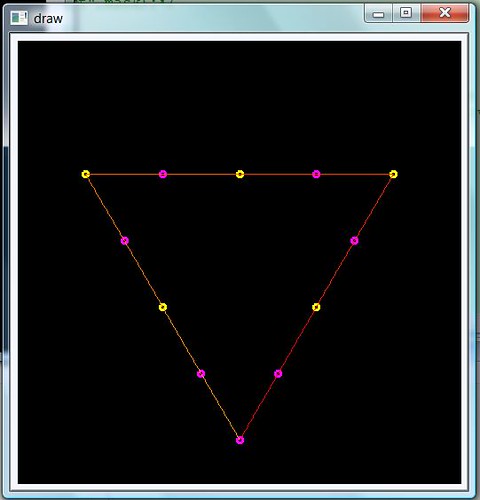
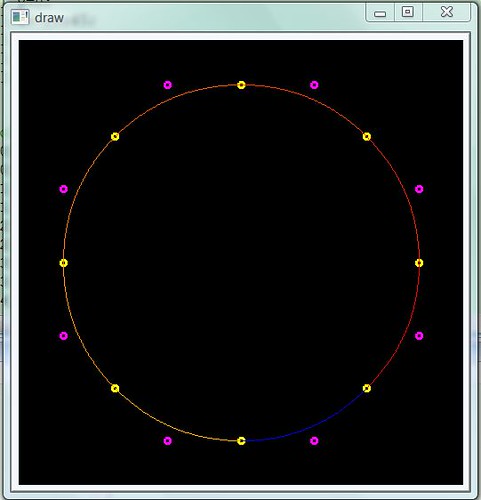
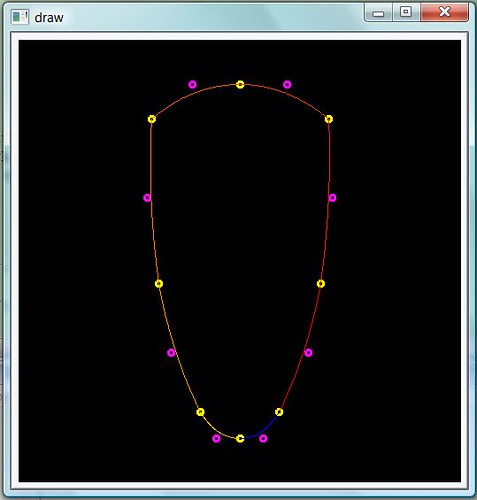
Coordinates

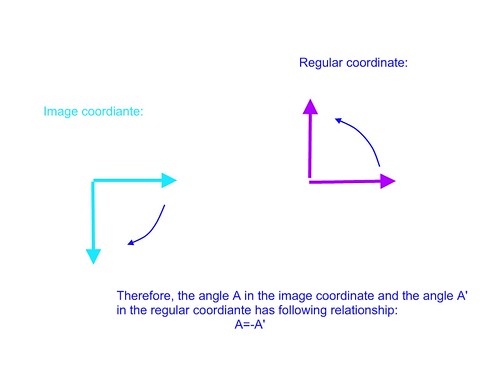
In Flash or image, the x-axis is the same to the one we use in math usually, which is called Cartesian coordinates. The exchange between them is simple:

Site: H-Anim

A site for humanoid animation. Specifications and so on.

http://h-anim.org/

Shape representation

Shape Representation.

Four basic shape using our representation:

A combined shape:

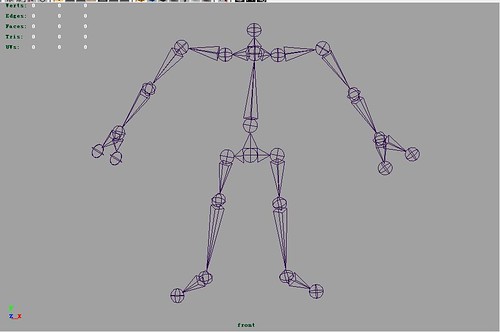
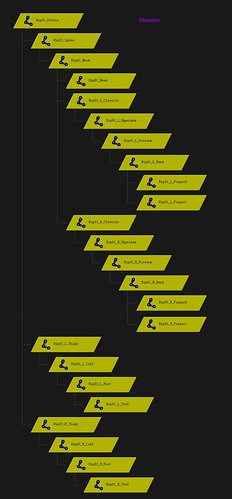
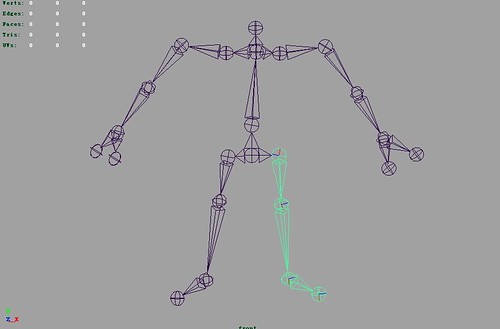
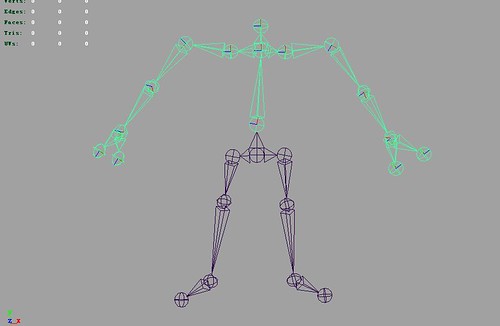
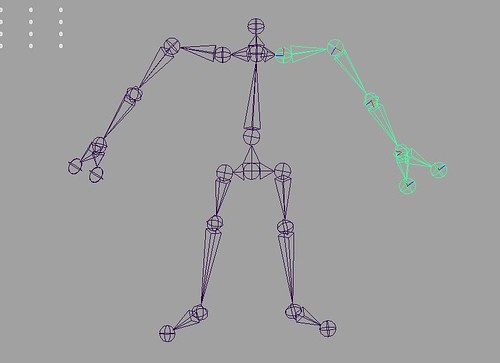
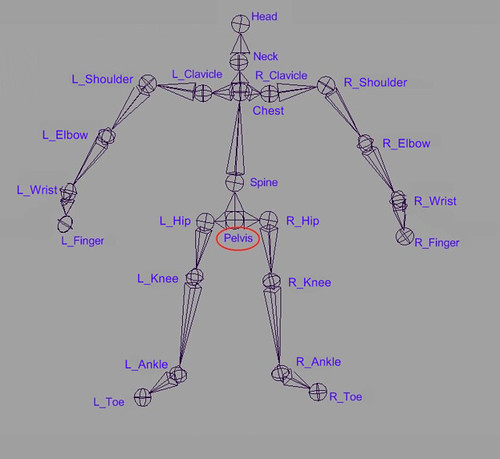
Skeleton used in Humanoid Animation

To animate the humanoid character, a well defined skeleton is used. Following is the skeleton we studied and used in our work.

The skeleton(using maya joint):

The hierarchy of this skeleton is:

The hierarchy also can be seen from following selections in Maya:

The annotated reference skeleton model is:

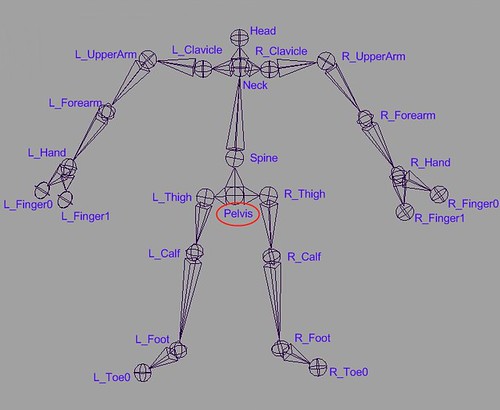
The one we use is slightly different in the neck area:

K-Sketch for animation

Thanks for David's seminar. http://www.k-sketch.org/

Their goal for this K-Sketch is:

Fast:

Simple:

Expressive: handle varieties of tasks

Related works:

Child tool: Sketchy    ....Simplicity

Professional Tool:      ....Expressive

Special Case Tool: Pivot Stick Figure Animator

KoKa,2005 A New Static Depiction and Input Technique for 2D Animation

Assist,2001 Resolving Ambiguities to Create a Natural Computer-Based Sketching ...

Race Sketch,2001 Animation Sketching: An Approach to Accessible Animation

18 animation operations

Change Goal to optimizations problems.

Evaluation:

Comfortable  level

Concepts & Techniques

Computational Geometry Code

This page lists "small" pieces of geometric software available on the Internet. Most of the software is available free of charge. Unless otherwise specified, C or C++ source code is available for all programs. Software libraries and collections and programs that can be run interactively over the web are listed on separate web pages.

Caveat Surfor! I can't make any claims about the usefulness or quality of the programs listed here. I don't have the time or equipment to try them all. If you have experience with any of these programs, either positive or negative, please tell me about it.

The programs on this page are divided into several categories, some of which are divided into further sub-categories. (Eventually, each category will get its own separate web page.) Each program is listed only once, but I've provided cross-links between overlapping categories, and I've tried to arrange similar categories near each other.

• Robust low-level primitives
• Combinatorics and discrete math
• Geometric optimization
• Convex hulls and convex polyhedra
• Voronoi diagrams and Delaunay triangulations
• Operations on polygons
• Mesh generation and manipulation
• Geometric modeling
• Visibility computation
• Visualization tools
• Other

Each category also includes links to relevant pages in Nina Amenta's comprehensive Directory of Computational Geometry Software, which I strongly encourage you to visit!

Items marked have been recently added or modified.

---

Robust low-level primitives

Avoid roundoff and precision errors! Use this code instead of naïve floating point or integer arithmetic.

• Relevant pages from DCGS:
  • Numerical and algebraic computation
• Ken Clarkson's Hull contains code to compute signs of determinants. See this paper for a description of his algorithms.
• Sylvain Pion's Modular package, based on the algorithms in "Modular Arithmetic for Geometric Predicates" by Hervé Brönnimann, Ioannis Z. Emiris, Victor Pan and Sylvain Pion.
• Adaptive precision floating point predicates used in Jonathan Shewchuk's Triangle package.
• Libraries for affine arithmetic and interval arithmetic (the first requires the second) from Jorge Stolfi's software collection
• Several algorithms to compute the exact sign of a deteminant (also here), collected by Mariette Yvinec. Part of the PRISME project at INRIA Sophia-Antipolis.
• The LEDA libraries includes code for exact arbitrary-precision integer, rational, floating point, and "real" arithmetic.

---

Combinatorics and discrete math

• LINK: A Software System for Discrete Mathematics under development at DIMACS
• Ulli Hund's program om2ps for visualizing oriented matroids as arrangements of pseudospheres. Sample output is available.
• Jorjeta Jetcheva's program to draw "clusters of stars", using an algorithm of Ileana Strienu (requires LEDA)
• Komei Fukuda's Reverse Search mathematica package for enumerating triangulations and connected induced subgraphs. Requires Steve Skiena's Combinatorica package.

---

Geometric optimization

• Relevant pages from DCGS:
  • Linear programming, smallest enclosing ball and center point
• Code by Ken Clarkson:
  • Fixed-dimensional linear programming
  • Approximate center points
• From Graphics Utilities by David Eberly:
  • Minimum enclosing circle
  • Minimum enclosing sphere (3d only)
• Mike Hohmeyer's implementation of Seidel's linear programming algorithm, courtesy of Seth Teller
• ANN: Library for Approximate Nearest Neighbor Searching, by David Mount and Sunil Arya
• Dave White's smallest enclosing ball software

---

Convex hulls and convex polyhedra

Most convex hull programs will also compute Voronoi diagrams and Delaunay triangulations. (Actually, all of them do, if you look at them the right way.)

Relevant pages from DCGS:

• Arbitrary dimensional convex hull, Voronoi diagram, Delaunay triangulation
• Low dimensional convex hull, Voronoi diagram and Delaunay triangulation

Low-dimensional convex hulls

• Two-dimensional convex hulls by Ken Clarkson
• From Graphics Utilities by David Eberly:
  • 2d convex hulls: conhull2.h, conhull2.c
  • 3d convex hulls: conhull3.h, conhull3.c
• ZRAM, a library of parallel search algorithms and data structures by Ambros Marzetta and others, includes a parallel implementation of Avis and Fukuda's reverse search algorithm.
• Geometric software by Darcy Quesnel:
  • Randomized parallel 3D convex hull, with documentation
  • 2D Delaunay triangulation, Voronoi diagram, and convex hull (requires LEDA)
• Harald Rosenberger's implementation of the beneath-beyond method for 3- and 4-dimensional convex hulls, courtesy of Ernst Mücke's GeomDir.

Arbitrary-dimensional convex hulls

• lrs 3.1: the first "official" distribution of David Avis' implementation of Avis and Fukuda's reverse search algorithm for vertex/facet enumeration. (This is an updated version of an earlier preliminary implementation.) An extensive user's guide is included.
• Qhull by Brad Barber, David Dobkin, and Hannu Huhdanpaa
  • Also available from this mirror site in Spain
  • The latest version (2.5) was released February 4, 1998.
• Primal-dual methods for vertex and facet enumeration by David Bremner, Komei Fukuda, and Ambros Marzetta
• Hull: Arbitrary-dimensional convex hulls, Voronoi diagrams, Delaunay triangulations, and alpha shapes, by Ken Clarkson
• PORTA, a collection of tools for analyzing polytopes and polyhedra, by Thomas Christof and Andreas Loebel, featured in Günter Ziegler's Lectures on Polytopes.
• Computational geometry software by Ioannis Emiris: perturbed convex hulls in arbitrary dimensions, exact convex hulls in two and three dimensions, mixed volume in arbitrary dimensions, and mixed subdivisions in the plane.
• Polytope software by Komei Fukuda
  • cdd and cdd+: arbitrary-dimensional convex hulls using Motzkin's double description method
  • A Mathematica package for Vertex enumeration of polytopes and arrangements
• Kurt Mehlhorn's programs for generating higher dimensional convex hulls and Delaunay triangulations and checking geometric structures. (C++WEB output only)

Measure properties

• Vinci (also here): a program for computing volumes of convex polytopes, presented as either the convex hull of a set of points, the intersection of a set of halfspaces, or both (with the vertex-facet incidence graph). Extensive online documentation and sample polytope files are available. Written by Benno Büeler, Andreas Enge, and Komei Fukuda.
• Ehrhart, a program to count integer points in convex polyhedra and compute Ehrhart polynomials, by Philippe Claus, Vincent Loechner, and Doran Wilde.
• Fast and accurate computation of polyhedral mass properties by Brian Mirtich, published in journal of graphics tools 1.2:31-50 (1996)

Boolean operations on polyhedra

• Polymake, a general-purpose polytope and polyhedron manipulation tool by Ewgenij Gawrilow and Michael Joswig Requires either cdd+, lrs, or porta for some computations and geomview for visualization. [C++ and Perl]
• Polylib, a library of polyhedral functions by Doran Wilde, includes code to compute convex hulls and perform boolean operations on unions of polytopes in any dimension.

Interesting and/or pathological polytope data

• Examples of pathological polytopes collected by David Bremner. See "How Good are Convex Hull Algorithms?" by Avis, Bremner, and Seidel for details. (data only)
• A collection of polytopes, mostly due to Günther Ziegler, from the polymake web site. (data only)

Miscellaneous

• A Mathematica package for unfolding 3D polytopes ( README) by Komei Fukuda; see "Strange Unfoldings of Convex Polytopes" for details.
• PUNTOS, a Maple package for computing triangulations of polytopes, regular triangulations of point sets, and their underlying oriented matroids, by Jesús de Loera
• Convex polyhedron code from a collection of mathematical programming software at the Konrad-Zuse-Zentrum für Informationstechnik, Berlin.

---

Voronoi diagrams and Delaunay triangulations

See also the implementation page from Christopher Gold's site www.Voronoi.com.

Relevant pages from DCGS:

• Arbitrary dimensional convex hull, Voronoi diagram, Delaunay triangulation
• Low dimensional convex hull, Voronoi diagram and Delaunay triangulation
• Medial axis and constrained Delaunay triangulation

Voronoi diagrams and Delaunay triangulations of points

Many convex hull programs can also compute Voronoi diagrams and Delaunay triangulations.

• 2d and 3d Delaunay triangulations by Jean-Daniel Boissonnat, Olivier Devillers, Stefan Meiser, and Monique Teillaud, from the PRISME project at INRIA Sophia-Antipolis.
• The Delaunay hieararchy, a data structure for 2d Delaunay triangulations that supports dynamic insertions (and deletions, but those aren't implemented), by Olivier Devillers, from the PRISME project at INRIA Sophia-Antipolis. (Solaris and SGI executables only)
• Graphics utilities by David Eberly:
  • 2d Delaunay triangulations: delaun2.c
  • 3d Delaunay triangulations: delaun3.c
• GAMBINI: a program for constructing multiplicatively weighted Voronoi diagrams for points in the plane, by Barry Boots. (Windows 3.1/95/NT executable only)
• Ernst Mücke's Detri, from his GeomDir, robustly computes 3D Delaunay triangulations.
• A simple divide-and-conquer Delaunay triangulation algorithm from Jorge Stolfi's software collection. Requires Stolfi'squad edge data structure library.
• Software by John Sullivan includes code to compute either standard Voronoi diagrams in Euclidean 3-space or periodic Voronoi diagrams in the 3-torus.
• Dave Watson's incremental convex hull/Delaunay triangulation program nnsort.c and a description of the algorithm
• Roman Waupotitsch's MinMaxer generates Delaunay, regular, and various other triangulations of two-dimensional point sets.
• Software on the Web, from the CNR-Pisa Visual Computing Group, includes code for 3D Delaunay triangulations

Constrained Delaunay triangulations

See also mesh generation and manipulation.

• Super Delaunay, a commercial fully dynamic constrained Delaunay triangulation package from David Kornmann (description only). Interactive demo versions for Sun Solaris and Linux are available here (binaries and data only). Demo versions for other architectures are available from the author.
• Dani Lischinski's incremental constrained Delaunay triangulation program CDT.
• Robert J. Renka's TRIPACK, Collected Algorithms of the ACM #751, computes constrained Delaunay triangulations, convex hulls, polygon areas, nearest neighbors, and shortest paths. (FORTRAN)

Medial axes and Voronoi diagrams of line segments

• Voronoi Diagrams of 2D Shapes by Martin Held. Robust computation of Voronoi diagrams and offset curves for planar shapes bounded by straight line segments and circular arcs. The web site only describes the software and illustrates some of the results; the code is available by email.
• Voronoi diagrams of line segments by Toshiyuki Imai (FORTRAN)
• Robert L. Ogniewicz's image skeletonization software
• avd, a LEDA extension package to compute abstract Voronoi diagrams in the plane, by Michael Seel. Code for Euclidean Voronoi diagrams of points and line segments is included.

Miscellaneous

• VoronoiImage by Marc Grundland: an image processing program that uses nested Voronoi diagrams to acheive stained-glass effects (Mac binaries only) [Warning: frames!]
• Alpha Shapes project at NCSA [Warning: frames!]
  • Online demo (also requires Java and VRML)
  • User's guide
  • Downloading instructions
  • Installation instructions
  • Documentation from Ernst Mücke's GeomDir

---

Operations on polygons

Relevant pages from DCGS:

• Medial axis and constrained Delaunay triangulation
• Polygons: decomposition, point location, intersection, visibility
• Triangulation

Point location

• Paul Bourke describes how to tell if a point is inside a polygon and how to calculate the area of a polygon, with C source code. From his Geometry pages.
• PNPOLY: William Randolf Franklin's point-in-polygon test, from the comp.graphics.algorithms FAQ
• Eric Haines' point-in-polygon code and experimental results from Ray Tracing News, Volume 5, Number 3. Newer, more optimized code is also available in Graphics Gems IV.

Boolean operations

• Constructive Planar Geometry by David Eberly: standard boolean operations on generalized polygons (only intersection is actually implemented)
• Boolean operations on polygons by Matej Gombosi.
• Boolean operations on sets of 2d polygons, by Klaas Holwerda, includes interactive visualization software (Sun and Windows only) and a complete description of the algorithms and data structures used. Results are "snap-rounded" to the integer grid.
• Polypack, a package of routines to manipulate polygons, by David J. Kennison (FORTRAN, description only)
• Alan Murta's generic polygon clipping library computes intersections, unions, and differences between possibly self-intersecting, possibly multiply-connected polygons, possibly with holes.
• Klammer Schutte's clippoly computes intersections and differences of nonconvex polygons. (Warning: The source contains over 10,000 lines of C++ code!)
  • An updated version of clippoly by Gregg Keichtman runs on a few more platforms than the original version. A Macintosh PowerPC executable and MATLAB versions are also available.
  • A much smaller version of the same algorithm, written in C by Alexy Nitikin and Michael Leonov, also handles polygons with holes. [New URL]

Triangulation and quadrangulation

See also the sections on Voronoi diagrams and Delaunay triangulations and mesh generation and manipulation.

• FIST: Fast Industrial-Strength Triangulation, by Martin Held, computes triangulations of polygons with holes, even in the presence of degeneracies or self-intersections. The web site only describes the software and illustrates some results; the code itself is avialable by email.
• Fast polygon triangulation code (also available here) by Atul Narkhede and Dinesh Manocha, published in Graphics Gems V, triangulates polygons in O(n log^* n) expected time using a randomized incremental algorithm of Raimund Seidel. Their code also handles polygons with holes.
• Polygon triangulation code by Ken Sloan, which optionally tries to merge as many triangles into quadrilaterals as possible.

Miscellaneous

• Thomas Auer and Martin Held's RPG implements several heuristics for randomly generating simple polygons from a given set of vertices. See also Auer's master's thesis.
• Source code from "Computing Common Tangents Without a Separating Line" by David Kirkpatrick and Jack Snoeyink (WADS 1995)

---

Mesh generation and manipulation

See also the sections on Delaunay triangulations and geometric modeling.

• Relevant pages from DCGS:
  • Mesh generation
  • Mesh manipulation
• Other collections:
  • Meshing programs, libraries and related programs collected by Christian Klesper for his extensive survey of meshing programs. [Warning: some parts of the survey require a frames-capable browser.]
  • Mesh generation software from Robert Schneiders' Mesh Generation & Grid Generation on the Web.
• Barry Joe's GEOMPACK (FORTRAN)
• Scott Mitchell's triangulation results includes code to generate linear-size nonobtuse triangulations of polygons, using the circle-packing algorithm of Bern, Mitchell, and Ruppert. (MATLAB and C++)
• EasyMesh by Bojan Niceno builds constrained and conforming Delaunay triangulations (and their dual Voronoi diagrams) and performs local mesh coarsening, refining, relaxation, and smoothing. Written by an applied physicist using algorithms developed by other applied physicists.
• Triangle, a comprehensive package by Jonathan Shewchuk for generating Delaunay triangulations and guaranteed-quality meshes.
  • Research credits, including Shewchuk's own paper about the program
  • Code for the adaptive precision floating point predicates used in Triangle are available separately.
• QMG: mesh generation and related software by Steven Vavasis
  • Source code (C++ and MATLAB)
• The Chopper, a semi-automatic hexahedral mesh generator, by the Finite Element Modelling Group, Queen's University of Belfast (descriptions only)
• STRIPE breaks a polygonal model into few triangle strips.

---

Geometric modeling

See also the section on mesh generation and manipulation.

Relevant pages from DCGS:

• Mesh manipulation
• Solid modeling
• Shape reconstruction
• Robotics

Binary space partition trees

• A BSP tree library in ANSI C, by A. T. Campbell, III; a slightly older version in C++ is also available.
• Bretton Wade's binary space partition tree source and demos for the Mac and Win95 machines. (An X version is reportedly in the works.) Several more BSP implementations are listed in his excellent BSP FAQ.
• Large geometric data sets, primarily models of Soda Hall, courtesy of Seth Teller.

Collision detection

• SOLID version 2.0: collision detection for moving three-dimensional objects, by Gino van den Bergen.
• Stephen Cameron's implementation of an algorithm of Gilbert, Johnson, and Keerthi to compute distances between convex polyhedra. Qhull is required for some features.
• Geometric software by Brian Mirtich:
  • V-Clip collision detection library
  • The Lin-Canny closest features algorithm
• A fast triangle-triangle intersection test by Tomas Möller, from journal of graphics tools, 2.2:25-30 (1997)
• Algebraic and geometric software from the UNC Research Group on Modeling, Physically-Based Simulation and Applications
  • I_COLLIDE: collision detection for convex polyhedra
  • RAPID: collision detection for arbitrary polygonal models

Reconstruction

• Surface reconstruction software by Hughes Hoppe and others, and accompanying range data for several 3d models
• Nuages, a package for 3D reconstruction from cross sectional data, from the PRISME project at INRIA Sophia-Antipolis

Simplification

• Michael Garland's terrain simplification programs scape and terra.
• Qslim: surface simplification code, using quadric error metrics, by Michael Garland
• Jade, a tool for simplifying triangular meshes, from the CNR-Pisa Visual Computing Group.
• Simplification Envelopes from the UNC Research Group on Modeling, Physically-Based Simulation and Applications

---

Visibility computation

• Heather Alef's X-windows visibility graph exploration tool
• Fast, minimum storage ray-triangle intersection by Tomas Möller and Ben Trumbore, from journal of graphics tools 2.1:21-28 (1997)
• VisPak: a package of visibility-related algorithms implemented by Helen Pinto and Lillanne Jackson at the University of Lethbridge. Requires LEDA to compile, but Sun binaries are provided.
• Michel Pocchiola and Gert Vegter's Greedy Flip Algorithm in Action, an implementation of the authors' algorithm for constructing visibility complexes by evolving pseudo-triangulations.
• Visibility Graphs and Motion Planning by Kittiphan Techakittiroj (Windows 3.1 executable only)

---

Visualization tools

You should also look for the thing being visualized! See also my list of programs that can be run over the web.

• Relevant pages from DCGS:
  • Visualization tools
  • Interactive visualizations
• UNREAL, a GeomView module for "hand-drawing" mathematical objects, by Nina Amenta, Danek Duvall, and Tim Rowley
• Javier Elices's GeomView module for visualizing the Dobkin-Kirkpatrick hierarchy
• Graphviz, tools for viewing and interacting with graph diagrams, by John Ellson, Eleftherios Koutsofios, and TopoVista: fly over USGS Digital Elevation Models, using right triangular irregular networks to maintain variable levels of detail, courtesy of Will Evans and Gregg Townsend. Requires OpenGL and Glut.
• DUST, a program for visualizing Voronoi diagrams, Delaunay triangulations, minimum spanning trees, and matchings in various metrics. From Michael Jünger's research group at Universität zu Köln.
• Peek by Gordon Kindlmann, a program for visualizing high-dimensional polytopes through their cross-sections and projections (or as Amenta and Ziegler would have it, their shadows and slices).
• Cinderellas Café, a "dynamic geometry" Java program written by Ulrich Kortenkamp and Jürgen Richter-Gebert, dynamically maintains sets of geometric objects (points, lines, circles, and conics) as the user moves their defining points around, provides primal and polar views of the same objects, supports spherical and hyperbolic geometry, and even includes some automatic theorem proving! A demo version is available. Information is currently available in German only.
• Geomview, the Geometry Center's 3d geometric visualization program, written by Stuart Levy, Tamara Munzner, Mark Phillips, and a cast of thousands. Also available from a mirror site in Berlin.
• JGV, a successor to GeomView written in Java, also from the Geometry Center. (Java, source not available)
• Bob Lewis's homogeneous coordinates and duality visualization program VideHoc (SGI executable only)
• Michael Murphy's Ranger, a program for visualizing high-dimensional nearest neighbor and orthogonal range searching data structures. From Steve Skiena's Practical Algorithm Reference
• The GeoPrO distributed visualization enviornment, by Pedro J. de Rezende, Guilherme Albuquerque Pinto, Alexandre Volpim, and Frederico Guth. (description only so far)
• Otfried Schwarzkopf's extendible drawing editor Ipe
• Toposcope: Automatic visualization of the topology of 2D cell complexes by Jorge Stolfi, Rober Marcone Rosi, C. F. Xavier de Mendonça, and L. P. Lozada
• Shastra, a geometric modeling and visualization system being developed at Purdue University (descriptions only)
• Software on the Web, from the CNR-Pisa Visual Computing Group, includes code for volume visualization.
• ZEUS, an algorithm animation system developed at DEC SRC (Modula-3)

---

Other

• Algorithms for partitioning multi-dimensional data sets, collected by Charles Alpert
• DemoKin, a demonstration of kinetic data structures for convex hulls, closest pairs, Voronoi diagrams, and minimum spanning trees, by Julien Basch, Leo Guibas, Craig Silverstein, and Li Zhang. Requires LEDA, XForms, and OpenGL to compile; an SGI executable is available.
• MAXRAD: software to find the maximum radius sphere touching each point (atom) in a set (molecule) using inversion and convex hulls, by Todd Yeates. (FORTRAN)

From: http://compgeom.cs.uiuc.edu/~jeffe/compgeom/code.html#mesh

Web 3D platform

Unity - A good commercial engine. Development only supports MacOS.

http://unity3d.com/

 

Blink 3D

http://www.pelicancrossing.com/index.htm

Commercial. Provides a free version.

 

Emma3D

http://emma3d.sourceforge.net/

Open-source.

Bezier Curves

Linear Bézier curves

Given points P₀ and P₁, a linear Bézier curve is simply a straight line between those two points. The curve is given by

and is equivalent to linear interpolation.

[edit]Quadratic Bézier curves

A quadratic Bézier curve is the path traced by the function B(t), given points P₀, P₁, and P₂,

A quadratic Bézier curve is also a parabolic segment.

TrueType fonts use Bézier splines composed of quadratic Bézier curves.

[edit]Cubic Bézier curves

Four points P₀, P₁, P₂ and P₃ in the plane or in three-dimensional space define a cubic Bézier curve. The curve starts at P₀ going toward P₁ and arrives at P₃ coming from the direction of P₂. Usually, it will not pass through P₁ or P₂; these points are only there to provide directional information. The distance between P₀ and P₁ determines "how long" the curve moves into direction P₂ before turning towards P₃.

The parametric form of the curve is:

Modern imaging systems like PostScript, Asymptote and Metafont use Bézier splines composed of cubic Bézier curves for drawing curved shapes.

 

Constructing Bézier curves

[edit]Linear curves

Animation of a linear Bézier curve, t in [0,1]

The t in the function for a linear Bézier curve can be thought of as describing how farB(t) is from P₀ to P₁. For example when t=0.25, B(t) is one quarter of the way from pointP₀ to P₁. As t varies from 0 to 1, B(t) describes a curved line from P₀ to P₁.

[edit]Quadratic curves

For quadratic Bézier curves one can construct intermediate points Q₀ and Q₁ such that as t varies from 0 to 1:

• Point Q₀ varies from P₀ to P₁ and describes a linear Bézier curve.
• Point Q₁ varies from P₁ to P₂ and describes a linear Bézier curve.
• Point B(t) varies from Q₀ to Q₁ and describes a quadratic Bézier curve.

Construction of a quadratic Bézier curve
Animation of a quadratic Bézier curve, t in [0,1]

[edit]Higher-order curves

For higher-order curves one needs correspondingly more intermediate points. For cubic curves one can construct intermediate points Q₀, Q₁ & Q₂ that describe linear Bézier curves, and points R₀ & R₁ that describe quadratic Bézier curves:

Construction of a cubic Bézier curve
Animation of a cubic Bézier curve, t in [0,1]

For fourth-order curves one can construct intermediate points Q₀, Q₁, Q₂ & Q₃ that describe linear Bézier curves, points R₀, R₁ &R₂ that describe quadratic Bézier curves, and points S₀ & S₁ that describe cubic Bézier curves:

Construction of a quartic Bézier curve
Animation of a quartic Bézier curve, t in [0,1]

(See also a construction of a fifth-order Bezier curve.)

 

 

From: http://en.wikipedia.org/wiki/Bézier_curve

ODOP

Density-based clustering methods: can discover clusters of arbitrary shape and filter out noises.

 

Preparing for the Qualification Examination, I found a sentence on the Operating System very meaningful.

"In biology, extinction is forever, but in Computer Science, it is sometimes only for a few years."

"An idea that is obsolete today may be the star of the party tomorrow!"

These words really emphasize the importance of the existing works in the field of computer science.

For my own case, the basic foundation in computer graphics is rather necessary!

Get more understanding of this area will give my research great foundation. Therefor, I plan to start my own work plan - ODOP (One Day One Paper)

So start work now, the first day begin!

News Digest Feb 12

Cognitive Computing Project Aims to Reverse-Engineer the Mind

Wired News (02/06/09) Ganapati, Priya

IBM Almaden Research Center cognitive computing project manager Dharmendra Modha has a plan to engineer the mind by reverse-engineering the brain.  Neuroscientists, computer engineers, and psychologists are working together to create a new computing architecture that simulates the brain's perception, interaction, and cognitive abilities.  The researchers hope to first simulate a human brain on a supercomputer, and then use new nano-materials to create logic gates and transistor-based equivalents of neurons and synapses to build a hardware-based, brain-like system.  The effort has received a $5 million grant from the Defense Advanced Research Projects Agency, which is enough to run the first phase of the project.  The researchers say if the project is successful it could lead to a new computing system within the next decade.  "The idea is to do software simulations and build hardware chips that would be based on what we know about how the brain and how neural circuits work," say University of California-Merced professor and project participant Christopher Kello.  The researchers started by building a real-time simulation of a small cerebral cortex, which has the same structure in all mammals.  The simulation required 8 terabytes of memory on an IBM BlueGene/L supercomputer.  Modha says the simulation, although not complete, offered insights into the brain's high-level computational principles.  A human cerebral cortex is about 400 times larger than the small mammal simulation and would require a supercomputer with a memory capacity of 3.2 petabytes and a computational capacity of 36.8 petaflops.  While waiting for supercomputing technology to improve, the researchers are working on implementing neural architectures in silicon.
http://blog.wired.com/gadgets/2009/02/cognitive-compu.html

CG Resource Links

Persons

http://graphics.stanford.edu/~levoy/ (a pioneer)

http://noll.uscannenberg.org/

http://physbam.stanford.edu/~fedkiw/ ( a large number of publication, simulation, G number of researchers)

http://people.csail.mit.edu/jovan/ ( Jovan Popovic)

 

 

http://graphics.stanford.edu/~hanrahan/ (rendering)

http://www.cs.cornell.edu/~srm/research.html ( he is more working on modelling)

http://www.cs.cornell.edu/~djames/research/index.html (his research has many about deformation processing)

http://www.cs.cornell.edu/~kb/ (her recently paper has some relations with perception)

http://www.cs.cornell.edu/~snavely/

 

 

University

MIT:

http://groups.csail.mit.edu/graphics/research.html

http://www.media.mit.edu/

Utah:

http://www.cs.utah.edu/research/areas/graphics/

http://www.cs.utah.edu/research/areas/percept/perception.html

Cornell:

http://www.graphics.cornell.edu/publications.html

Stanford:

http://graphics.stanford.edu/

 

Brown:

http://graphics.cs.brown.edu/home.html

http://graphics.cs.brown.edu/games/

Using OpenCV

After installation, you must add "{installation folder}/OpenCV/bin" and "{installation folder}/OpenCV/lib" to the system environment path.

In Visual Studio, add "{installation folder}/OpenCV/cv/include", "{installation folder}/OpenCV/cxcore/include", "{installation folder}/OpenCV/ml/include" and "{installation folder}/OpenCV/otherlibs/highgui" to Tools->Options->Projects and Solutions -> VC++ Directories :Include files.

Moreover, add "{installation folder}/OpenCV/lib" to library files.

Then, open the property dialogue of the project, add "highgui.lib cv.lib cxcore.lib ml.lib" to Linker-> Input.

Photography tips

根据人物的感觉和性别区分使用曝光补偿

曝光补偿的基本原理已经在上述内容中进行了说明，在拍摄人物时如果皮肤反射率较高，有可能也需要进行曝光补偿。这时应根据皮肤色调选择补偿方向。通常情况下，女性的皮肤即使未经化妆也比较白皙。因此采用相机自动模式进行拍摄有可能会偏黑。这样一来，拍摄对象可就会大为不满了。这时候可以进行正方向补偿，使皮肤变得明亮，才会讨人喜欢。而且曝光补偿可使脸上的斑点和皱纹也变得不那么显眼了，效果非常突出。相反，以男性为拍摄对象时，可以稍微进行负方向补偿，这样可以使人显得更加坚毅。曝光补偿并不只是选择正确的数值，也是对亮度进行调节，从而获得良好的整体图像效果的手段。因此这是一种优先考虑拍摄者自身所希望呈现出的图像效果的技巧。

对黑色被摄体向负方向进行曝光补偿

对白色被摄体向正方向进行曝光补偿

提高ISO感光度时图像质量会降低

昏暗部分的噪点比明亮部分的更加明显

如图所示，ISO感光度与画质之间有着密切的联系。提高ISO感光度时产生噪点的原因之一是在对影像信号进行增幅时混入了电子噪点。如果希望保持尽可能高的画质，应该使用低ISO感光度。但低感光度拍摄昏暗的室内或夜景，快门速度会非常低，所以需要注意很容易产生手抖动和被摄体抖动。此外，噪点本身有在昏暗部分比明亮部分更显眼的倾向。所以在室外明亮处拍摄照片时候将感光度提升到ISO 400 噪点不会太醒目。越提高ISO感光度快门速度就越高，可以有效防止手抖动和被摄体抖动。但在使用高感光度的时候，要注意画质劣化的问题。

根据直方图数据读取所需的必要信息

像前面所说过的一样，直方图是对整体亮度进行统计学显示，即使其分布状态均匀也不能绝对地说曝光就一定正确、合适。拍摄白色沙滩上的白色冲浪板时，即使直方图极端偏右也没有什么好奇怪的。相反，如果光凭直方图来判断夜景时的曝光，波峰会向左方偏移得十分厉害，感觉整个图像都是暗部缺失才对。这时最重要的是明确要从直方图中读取什么内容，只要能确认是否有暗部缺失或高光溢出等必要信息，就不必对图形整体分布趋势过于敏感。直方图作为用于确认无法预测的高光溢出或暗部缺失的手段使用也不错。

● 人物与背景保持一定距离比较有利

● 利用远摄端的特性减少背景

● 最理想的是同时使用与背景的距离＋远摄端

● 利用距镜头越近看上去越大的特性

● 广角端是显得人腿最长的焦距

● 以人物为优先来考虑拍摄位置

● 大人降低到儿童视线高度位置

● 如果想拍摄全身可以另行拍摄

● 仔细安排人物以突出主角

晴天人物摄影：逆光+反光板

夜景拍摄：

● 最好的拍摄时间是在完全天黑前

● 白平衡用目测决定

● 曝光补偿用负的使之更暗

防止抖动同时减少映射，灵活使用自拍功能

拍摄首饰时，也要使用能让画质更漂亮的ISO 80左右的低感光度。此外拍摄光源使用能自由改变角度的台灯虽然方便，但很多时候明亮度并不理想。而荧光灯的光线与数码相机自动白平衡的相性比较好，是推荐使用的道具。不过这样快门速度会变慢，需要防止手抖动，为此准备了可以在桌上使用的迷你三脚架。拍摄使用微距模式，对焦于希望展示的部分，靠近拍摄特写。这次的被摄体比较小，因此使用了能够拍出更大画面的广角端，然后仔细对焦后拍摄即可。然而如之前所料，快门速度相当慢，即使使用了三脚架也还是不太放心。于是使用了自拍功能，注意不给相机带来冲击。此外在拍摄首饰类有光泽的反光物体时，可能操作相机的拍摄者会映到被摄体上。因此通过使用自拍功能，拍摄者可离开相机拍摄，十分方便。

以色彩为表现中心的被摄体不适合黑白拍摄

黑白照片的玩法虽说是自由的，但由于不包含色彩信息，确实存在被摄体合不合适的问题。旅游的回忆，以及家庭照片等以记录为主要目的的拍摄，可以说不太适合黑白。但也有许多被摄体都可以用黑白来表现，例如稍微具有怀旧氛围的旧街，还有人像等。黑白是用黑与白的浓淡来表现色彩，所以花朵等以色彩为表现核心的东西不适合黑白。拍摄时要考虑被摄体的色彩与表现的平衡。

Drawing books

Technical Drawing - rev3

Publish at Scribd or explore others: Academic Work Science & Engineerin Science-Engineering Technical

 

Andrew Loomis - Successful Drawing

Publish at Scribd or explore others: Internet & Technolog Health & Medicine easy drawing

 

How to Draw Anime

Publish at Scribd or explore others: Education eBooks Education-eLearningO draw anime game char

Drawing Guide

Drawing Guide

Publish at Scribd or explore others: Manuals Education drawing Simple

News Digest Feb 10

Google Makes it Easy to Spy on Kids, Workers

Associated Press (02/05/09) Liedtke, Michael

Google recently upgraded its mobile maps software with a feature called Latitude that allows users with mobile devices to automatically share their location with others.  The feature expands on a tool released in 2007 that allows mobile phone users to check their own location on a Google map.  The new feature raises several security concerns, but Google is trying to address this issue by requiring each user to manually turn on the tracking software and making it easy to turn off or limit access to the service.  Google says it will not retain any information on its users' movements, and that only the last location recorded by the tracking service will be stored on Google's computers.  The software uses cell phone towers, global positioning systems, or a Wi-Fi connection to find users' locations in the United States and 26 other countries.  Each user can decide who can monitor their location.  Latitude will initially work on Blackberrys and devices running on Symbian software or Microsoft's Windows Mobile.  Eventually the software will be able to operate on some T-1 Mobile phones running Google's Android software and Apple's iPhone and iTouch devices.  Google also is offering a PC version of the feature.  The PC program will allow people who do not have a mobile phone to find the locations of contacts or keep track of their children.
http://www.rdmag.com/ShowPR.aspx?PUBCODE=014&ACCT=1400000101&ISSUE=0902&RELTYPE=SOFT&PRODCODE=00000000&PRODLETT=BU&CommonCount=0

 

UAHuntsville Lab Combines Psychology With Technology for Unique Research Projects

University of Alabama in Huntsville (02/02/09) Maples, Joyce

University of Alabama in Huntsville (UAHuntsville) professor Anthony Morris directs the school's Human Factors and Ergonomics Laboratory, which combines psychology and technology to research work performed by human factors engineers.  Experimentation and research projects include human operator interactions with complex systems such as aircraft, and designing work stations that are logical, user friendly, and can help prevent injuries.  For example, Morris and UAHuntsville graduate student Sage Jessee have been working with the Human Research and Engineering Directorate of the Army Research Lab to evaluate the head and eye movements of Black Hawk helicopter pilots.  The project involved using eye-tracking in a video game-like simulator to monitor the pilot's point of gaze and head position during flight scenarios.  The researchers created an "attentional landscape" that characterized the general gaze of the pilot, and identified specific eye measures that correlate with mental workload.  The result of the project was a new ergonomically designed cockpit that enabled pilots to spend 90 percent of their time looking outside windows instead of continuously staring at the instrument panel.
http://www.uah.edu/News/newsread.php?newsID=1283

A survey of shape analysis techniques

This paper, published in 1998, is about the techniques in shape analysis. It talked about shape representation and description aspects of shape analysis.

Briefly introduction about Human Perception of Visual Form.

Boundary space & Body space techniques.

Polygonal & Spline approximations.

Medial axis.

 

This paper started from the human visual perception to introduce a large amount of shape analysis techniques. A good overview of shape analysis techniques.

 

[1998]a survey of shape analysis techniques

Publish at Scribd or explore others: Academic Work Research paper shape analysis

 

Useful papers from reference:

39. Decomposition of three-Dimensional objects with spheres.

40. Minimal rectangular partition of digitalized blobs.

48. Visual Perception

61. Visual cognition: an introduction, Cognition

139. Shape design, representation, and restoration with splines.

145. An Introduction to Splines for use in Computer Graphics.

173. Ordered structural shape matching with primitive extraction.

[Lyrics] Owl City - The Saltwater Room

I opened my eyes last night and saw you in the low light 
Walking down by the bay, on the shore, staring up at the planes that aren’t there anymore 
I was feeling the night grow old and you were looking so cold 
Like an introvert, I drew my over shirt around my arms and began to shiver violently 
Before you happened to look and see the tunnels all around me 
Running into the dark underground 
All the subways around create a great sound 
To my motion fatigue: farewell 
With your ear to a seashell 
You can hear the waves in underwater caves 
As if you actually were inside a saltwater room 

Chorus: 
(Time together is just never quite enough) 
When you and I are alone, I’ve never felt so at home 
(What will it take to make or break this hint of love?) 
We need time, only time 
(When we’re apart whatever are you thinking of?) 
If this is what I call home, why does it feel so alone? 
(So tell me darling, do you wish we’d fall in love?) 
All the time, all the time 

Can you believe that the crew has gone and wouldn’t let me sign on? 
All my islands have sunk in the deep, so I can hardly relax or even oversleep 
I feel as if I were home some nights when we count all the ship lights 
I guess I’ll never know why sparrows love the snow 
We’ll turn off all of the lights and set this ballroom aglow 
(So tell me darling do you wish we'd fall in love) 
(All the time) 

Chorus: 
(Time together is just never quite enough) 
When you and I are alone, I’ve never felt so at home 
(What will it take to make or break this hint of love?) 
We need time, only time 
(When we’re apart whatever are you thinking of?) 
If this is what I call home, why does it feel so alone? 
(So tell me darling, do you wish we’d fall in love?) 
All the time, all the time 

(Time together is just never quite enough) 
(When we're apart whatever are you thinking of?) 
(What will it take to make or break this hint of love?) 
(So tell me darling do you wish we'd fall in love) 
(All the time)